Help with those 'Simple Rules.'
The instructions for a traditional Sudoku puzzles are simple: Place all of the elements 1 through 9 exactly once in each row, column, and 3x3 square. The beauty, as well as the challenge, of all types of group logic puzzles like Sudoku is the minimalist nature of these rules. Knowing how to check for a correct solution, however, does not mean that the solution is easy to logically deduce.
In fact, the class of computer science problems that have a simple solution check but no known optimal algorithm are proven to be the most difficult class of problems to solve, with the optimal solutions requiring guessing correctly at every possible choice point. For these types of puzzles, there does not exist a single set of rules or algorithm that will always produce a set of solution steps that leads the solver deductively from puzzle to solution, for every possible puzzle that has a solution. Thus, computers and humans alike, must guess at solutions for certain Sudoku and Group Puzzles and check the group constraints to see whether the solution is in fact valid. Although computers can guess, check, and backtrack quickly if they are wrong, puzzles designed to be worked by humans should not require guessing or backtracking if the purpose is to teach deductive logic. For teaching purposes, puzzles should be selected only if there exists a sequence of deductive step-by-step moves that lead from the puzzle to the solution.
Although there does not exist a simple definitive set of rules for deductively solving all puzzles, there do exist general strategies, which computer scientists often call heuristics, that can be used to solve most puzzles. For Group Puzzles there are two basic strategies that encompass most of the strategies in common use: find the only spot in a particular group where a certain value can occur (given the group constraints) and find the only value that can be placed in a particular spot (given the group constraints).
Strategy 1.
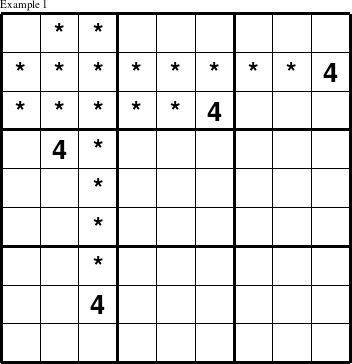
The first and most common approach to solving these puzzles is to figure out all the spots in a constraint group where a particular value cannot be placed, and when there is only one spot left in the group where it is allowed, you have found the spot where the value must be put. To do this, check if one value in the puzzle appears in several places and constrains where that value can appear in another group. In example 1, the value 4 must appear at the
top of the first column at coordinates (1, 1) because the value 4 appears outside the 1st 3x3 square (top left 3x3 square) in rows 2 and 3 as well as columns 2 and 3. So, the only spot left for 4 in the 1st 3x3 square is at (1, 1).
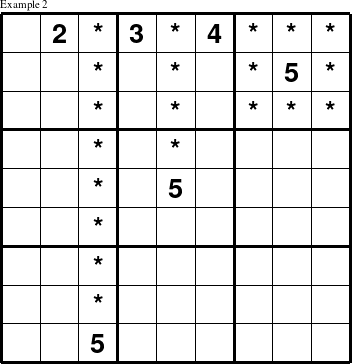
Although the application of this technique to 3x3 squares is by far the most common way for people to work towards a puzzle solution, the same logic applies to rows and columns as well. In the next puzzle, the value 5 must appear at (1, 1) because the 5 in the second row means that 5 cannot appear in the last 3 columns of row 1, and the 5 in the fifth row means that it cannot appear in column 5 of row 1. Furthermore, the 5 in the last row rules out a 5 in column 3, and there are already values of 2, 3, and 4 in the second, fourth, and sixth columns of row 1.
Thus, the only spot left for 5 in the 1st row is at (1,1).
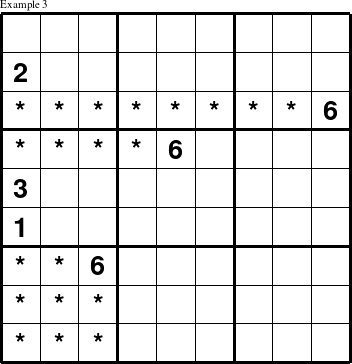
The values in columns can be similarly deduced. In the puzzle below, a 6 must be placed at (1, 1) because the value 6 in the third column eliminates the last three rows as spots for a 6 in column 1, and the values 1, 2, and 3 in column 1, as well as the 6s in columns 5 and 9, rule out the remaining spots.
Thus, the only spot left for 6 in the 1st column is at (1,1).
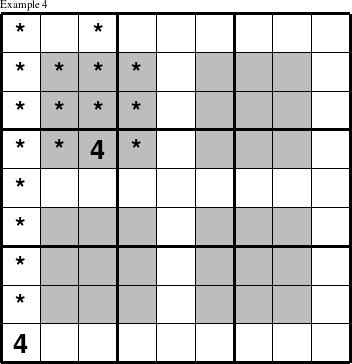
This same strategy can be used to deduce values in other types of Group Puzzles as well. In the HyperSudoku puzzle below, the four inner squares that are colored gray are additional groups that must also contain the values 1 through 9.
Here, the only spot left for a 4 in the 1st 3x3 square is at (2, 1), because the 4 in the last row rules out all of the spots in the first column, and the 4 in the fourth row rules out all of the gray squares and the third column of the 1st 3x3 square. Additional groups, like the inner 3x3 squares, provide additional constraints that make this strategy more effective with fewer givens; only two 4s outside the completely empty 1st 3x3 square were required to determine where in the 1st 3x3 square the 4 must be placed.
Strategy 2.
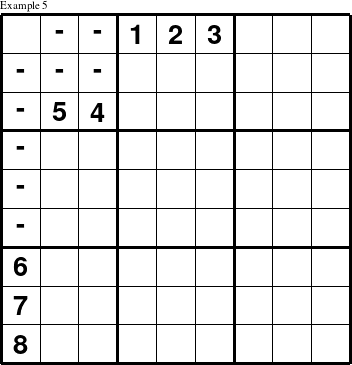
Another strategy that is useful in some puzzles is to determine what values cannot possibly be placed in a particular spot, and if there is only one possible value left, then the spot must hold that value. The values that cannot appear in a spot can be determined by finding all the values that already appear in any of the groups that include the spot. Thus, in example 5 below, a 9 must be placed at (1, 1) because it is the only value left that is not already in the 1st 3x3 square, the 1st column or the 1st row.
A 1, 2, or 3 placed at (1, 1) would conflict with the values in row 1. Similarly, a 6, 7, or 8 would conflict with the values in column 1 and both a 4 and 5 can already be found in the 1st 3x3 square. This strategy is often called counting in Sudoku puzzle solving guides.
Strategy 3.
One deterministic strategy that is often found in advanced Sudoku puzzle solving guides under a wide variety of names is illustrated in the puzzle below. Since only 8 and 9 are missing from the second 3x3 square, they must both be located in the third row, even though which number goes where in the two empty spots cannot yet be determined. This, however, implies that there must be an 8 in the third row in the 2nd 3x3 square, and that 8, therefore, cannot appear in the third row of either the 1st or 3rd 3x3 squares. Additional constraints shown in the puzzle imply that 8 cannot be placed anywhere in the 1st 3x3 square other than at (1, 1).
Unlike the previous techniques that apply equally to rows and columns, this one can only be used when there are two groups that overlap in at least two spots. Thus it can only be applied to 3x3 squares and rows or 3x3 squares and columns in a traditional Sudoku puzzle, because any two rows and columns overlap only in one spot. In the published puzzles that have been evaluated to date, this deterministic strategy has not proven necessary to solve puzzles when the first two deterministic methods are combined. Any moves determined by this strategy can almost always be determined by using only the first two methods, although each empty spot cannot necessarily be determined at the same point in the solution. For this reason, this third strategy is not currently used in the puzzle difficulty key algorithm used to rate puzzles. If a puzzle were designed so that this strategy was required when the first two were insufficient to make progress toward the solution, the current puzzle difficulty algorithm would search for a nondeterministic guess that would allow for a solution. Thus, in effect, the puzzle rating system would rate this or any other type of deterministic strategy that was not implemented in the rating algorithm as a nondeterministic step.
Nondeterministic Strategies.
The strategies listed so far are all deterministic because they allow the value to be logically determined without any question or doubt so long as no mistakes have been made in the puzzle. Another technique is called nondeterministic or more colloquially, "guess and check," because it requires guessing that a step is correct without any logical guarantees that it is correct. Nondeterministic steps may not lead to a solution and may in fact lead to a contradiction in the sense that you may reach a point where no value is valid for a spot. If all of your other steps before and after your guess were deterministic and based solely on logic, then by reaching a contradiction you have logically shown that your guess was incorrect and that the value cannot be placed in the spot specified by your guess. Multiple guesses are much more complex and require negative results on all possible combinations to draw any conclusions about the validity of the initial guess. Nondeterministic algorithms that check all possible guesses are often used by computers to solve these puzzles. This technique, however, often proves difficult and error prone for most human solvers. Nevertheless, some puzzles are published that require a nondeterministic step (or guess) and if you reach a point in the solution of a puzzle where it seems that you cannot make any further deterministic progress, you may need to make a guess at that spot and backtrack to the exact same puzzle where you made your guess if you eventually reach a contradiction. Multiple levels of guesses have never proven necessary to solve and rate any published puzzles tested to date. Indeed, many argue that it is not a valid Sudoku puzzle unless there exists a deterministic solution that does not require guessing.
Although there are many other types of deterministic and nondeterministic strategies that can be used to solve these types of puzzles, the two deterministic strategies described above and in the section on computing difficulty keys have been found to be sufficient to solve the vast majority of the published puzzles tested so far. By allowing a single guess (nondeterministic step), all published puzzles tested have been solved. This indicates that these two deterministic strategies are general enough to replace all of the rules and patterns that make up most Sudoku strategy guides.